분류 문제를 회귀로 해결하는 알고리즘이 있습니다.
이번 글에서는 이진분류가 가능한 로지스틱 회귀와, 다중분류를 할 수 있는 소프트맥스 회귀에 대해서 알아보겠습니다.
먼저 로지스틱 회귀에 대해서 알아보도록 하겠습니다.
로지스틱 회귀는 이진분류만 가능합니다.
추정확률을 반환하여 50% 이상이면 1, 아니면 0으로 분류하게 됩니다.
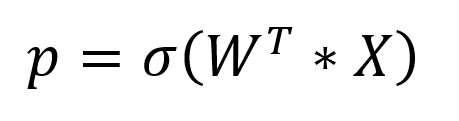
처음 보는 저 기호는 sigmoid입니다.
sigmoid는 0과 1 사이의 값으로 변환해주는 앞으로 많이 보게 될 유용한 함수입니다.
시그모이드는 다음과 같습니다.

로지스틱 회귀의 예측 식에 대해 알아보았으니 비용함수에 대해 알아보도록 합시다.
한 훈련사례에 대해서는 다음과 같습니다.

전체 비용함수는 다음과 같이 정리할 수 있습니다.

편도함수는 다음과 같습니다.

위와 같은 편도함수를 이용하여 최적의 가중치를 찾아내며 로지스틱 회귀로 모델을 학습시킬 수 있습니다.
자 다음으로는 다중분류가 가능한 소프트맥스 회귀에 대해서 알아보도록 하겠습니다.
소프트맥스는 각 클래스에 점수를 계산하고 그 점수에 소프트맥스 함수를 적용하여 확률을 추정합니다.
다음의 수식과 같이 점수를 계산합니다.

클래스 k에 대해서 각각 가중치들이 존재합니다.
점수를 구했다면 각 점수를 소프트맥스 함수를 이용하여 확률로 반환해야 합니다.
소프트맥스 함수는 다음과 같이 확률로 반환합니다.

k 클래스의 확률 p는 위와 같습니다.
소프트맥스 회귀는 p값이 제일 높은 k클래스로 예측하게 됩니다.
이제는 소프트맥스 회귀의 비용함수로 쓰이는 크로스 엔트로피를 설명하도록 하겠습니다.
크로스 엔트로피는 다중분류에서 널리 사용되는 비용함수입니다.

위의 크로스 엔트로피 식에서 K=2 이면 처음 로지스틱 회귀의 비용함수와 동일합니다.
이제 크로스 엔트로피의 Gradient Descent Vector에 대해 알아보겠습니다.

k클래스에 대한 가중치의 GradientDescentVector는 위와 같습니다.
위 식을 이용하여 소프트맥스 회귀 모델을 학습시킬 수 있습니다.