심층 신경망을 학습하게 되면 다양한 문제가 존재하게 됩니다.
오늘은 그중에 그래디언트 소실, 폭주 그리고 과대적합 문제에 대해서 다뤄보도록 하겠습니다.
그래디언트 소실은 역전파 과정에서 하위층에 있는 뉴런들에 전해지는 loss는 적어, 일찍 수렴해버리는 문제입니다.
그리고 그래디언트 폭주는 그래디언트 소실과 반대로 하위층에 있는 뉴런들에 전해지는 loss가 너무 커져버리는 문제입니다.
이런 문제들을 해결하기 위해 가중치 초기화 방법을 바꾸거나, 새로운 활성화 함수를 이용합니다. 또는 배치 정규화를 이용합니다. 그래디언트 클리핑으로 폭주문제를 해결할 수도 있습니다.
오늘은 앞서 말씀드린 문제들을 해결하는 총 6가지 방법에 대해 알아보겠습니다.
먼저 새로운 가중치 초기화 방법에 대해 말씀드리겠습니다. (이번 글에서는 아주 간단히 설명하고 넘어갑니다.)
학습 초기에 발생하는 그디언트 소실, 폭주 문제를 크게 완화해줍니다.
tanh, sigmoid, softmax 등의 활성화함수에서 좋은 성능을 보이는 글로럿 초기화(세이비어 초기화)와
ReLU 함수와 ReLU와 비슷한 함수들에서 좋은 성능을 보이는 he 초기화가 존재합니다.
(ReLU함수의 변종중에 하나인 SELU에서는 르쿤 초기화를 사용하기도 합니다.)
새로운 활성화함수를 이용하여 이 문제를 완화하기도 합니다.
수렴하지 않는 활성화함수인데요, 이번 글에서 알아볼 새로운 활성화함수는 ReLU에서 변종되었습니다.
바로 LeakyReLU입니다.
ReLU와 LeakyReLU 함수식을 보면 다음과 같습니다.

LeakyReLU에는 새로운 하이퍼파라미터가 추가됩니다. a 파라미터는 활성화함수의 x값이 음수일때 그래프가 가지는 기울기입니다.

위의 사진은 ReLU 함수의 그래프 개형입니다.

위 사진은 LeakyReLU 함수의 그래프 개형입니다.
ReLU의 경우에는 x < 0 일때 기울기가 0이 되는데, LeakyReLU는 그렇지 않습니다.
이런식으로 활성화함수를 변경하여 그디언트 소실, 폭주 문제를 완화할 수도 있습니다.
그 다음으로는 배치 정규화(Batch Normalization)입니다.
배치 정규화의 과정을 수식으로 정리하여 보겠습니다.

맨 위에 있는 수식은 평균이고, 그 다음 수식은 분산을 구하는 것입니다. m_B 는 미니배치 샘플 수입니다.
세번째 수식에 3을 좌우반전 시켜놓은 듯한 epsilon은 분모가 0이 되는 것을 막아주는 아주 작은 상수입니다.
세번째 수식과 네번쨰 수식을 거쳐 배치정규화 결과를 도출해냅니다.
배치정규화를 진행함으로서 결과값들의 분포를 학습이 잘되는 쪽으로 다시 뿌려주는 것입니다.
Batch Normlization도 다른 은닉층과 같이 층을 새로 추가하는 형태로 학습하게 됩니다.
하지만 Batch Normlization의 문제점이 있습니다. 바로 예측을 어떻게 할것인가에 대한 문제입니다.
항상 미니배치 샘플 수만큼의 예측샘플을 사용하는 것은 좋지 못한 방법일 것입니다.
배치 정규화 기법을 처음 제안한 Sergey Ioffe, Christian Szegedy는 모델을 학습하면서 구했던 평균과 분산의 이동평균을 이용하였습니다. (참고: https://ko.wikipedia.org/wiki/%EC%9D%B4%EB%8F%99%ED%8F%89%EA%B7%A0)
배치 정규화는 학습 시간을 줄여주고, 모델의 일반화에도 많은 도움이 됩니다.
그래디언트 폭주 문제를 완화하는 방법에는 그래디언트 클리핑이 있습니다.
그래디언트 클리핑은 그래디언트 값이 일정 임곗값을 넘지 못하도록 하는 것입니다.
간단하지만 효과적인 방법으로 인기있는 아이디어입니다.
모델의 훈련속도를 높이는 새로운 옵티마이저인 Adam에 대해서 알아보겠습니다.
Adam은 모멘텀 최적화와 RMSProp을 결합한 알고리즘으로 현재 가장 인기있는 최적화 알고리즘입니다.
먼저 모멘텀 최적화에 대해서 알아보도록 하겠습니다.
기존의 경사하강법과는 다르게 모멘텀 최적화는 가중치 업데이트에 가속도가 존재합니다.
수식으로 보면 더 이해가 빠를 것 입니다.

m을 그래디언트 벡터로 업데이트하고, 업데이트된 m으로 가중치를 업데이트하는 방식입니다.
이 방법을 이용하면 학습시간이 매우 빨라집니다.
이제 RMSProp에 대해 알아보겠습니다.
RMSProp은 모멘텀 최적화와 반대로 가중치 업데이트를 점점 낮춥니다.
수식으로 보면 다음과 같습니다.

학습률을 점점 줄이는 것입니다.
이제 원래 알아보려고 했던 Adam에 대해 설명하도록 하겠습니다.
Adam은 학습률을 높이는 모멘텀 최적화와 학습률을 줄이는 RMSProp을 동시에 사용하는 것입니다.
수식은 다음과 같습니다.
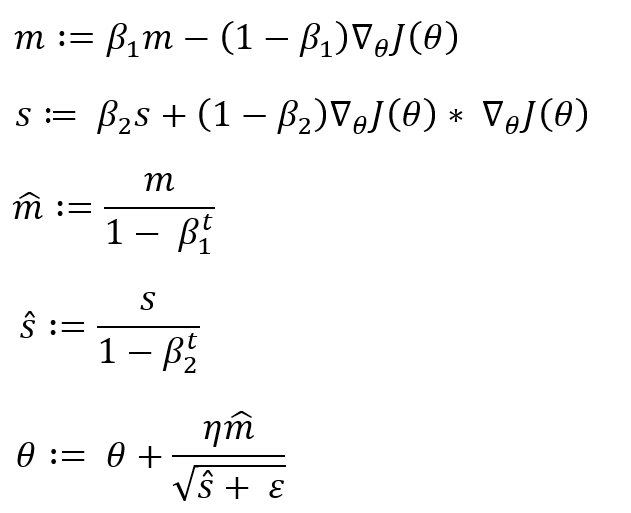
첫번째와 두번째 수식은 익숙합니다. 모멘텀 최적화와 RMSProp과 매우 유사한 식입니다.
세번째와 네번째 수식은 가장 처음 0으로 초기화되는 m과 s가 0쪽으로 너무 치우치지 않게 증폭시키는 식입니다. t는 반복횟수입니다. 반복횟수가 늘어날수록 더 이상 증폭되지 않을 것입니다.
가중치 업데이트 속도를 늘였다가 줄이는게 무슨 경우인지 어이가 없을 수 있겠지만, 이는 실제로 잘 작동합니다.
마지막으로 심층 신경망의 과대적합을 해결하는 훌륭한 알고리즘인 드롭아웃에 대해서 알아보도록 하겠습니다.
드롭아웃은 하나의 뉴런이 모델전체에 너무 많이 기여하지 않도록 하는 것입니다.
예를 들어 한 회사에 그저그런 직원 9명과 아주 똑똑한 직원 1명이 있다고 생각해봅시다. 어떤 일에 결정을 할 때 직원 9명은 아주 똑똑한 1명의 결정에만 무조건적으로 따릅니다.
하지만 이에는 큰 문제점이 있습니다. 아주 똑똑한 1명이 실수로 잘못된 판단을 할 수도 있고, 몸살이 나 회사에 출근하지 못하는 경우도 있을 것입니다. 총 10명중 1명이 출근을 못했다면 일반적으로 원래의 90% 일을 해야할텐데, 그보다 아주 작은 5%일지도 모르겠습니다.
이처럼 드롭아웃은 하나의 뉴런이 모델 전체에 너무 많이 기여하지 않도록 규제합니다. 학습하는 동안 몇개의 뉴런들을 일정확률로 제외시키면서요.
드롭아웃은 각 뉴런이 한 에포크에서 제외될 확률, 드롭아웃 비율을 하이퍼파라미터로 갖습니다.
이는 아주 효과적인 규제방법입니다. 순환신경망에서는 대부분 20%~30%로 설정하고, 합성곱 신경망에서는 대부분 40%~50%로 설정합니다.
이렇게 오늘은 심층신경망의 여러 문제를 완화하는 글로럿, he 초기화, LeakyReLU, 배치 정규화, 그래디언트 클리핑, Adam, 드롭아웃에 대해서 알아보았습니다.
'인공지능 > 이론' 카테고리의 다른 글
| (19) RNN 구조 (0) | 2022.01.02 |
|---|---|
| (18) 컴퓨터 비전 (0) | 2021.11.12 |
| (16) 인공 신경망 (0) | 2021.10.24 |
| (15) 비지도학습 (0) | 2021.10.23 |
| (14) 차원 축소 PCA (0) | 2021.10.22 |



